Section A.2 Batting Average Puzzle
A player’s batting average during a chosen time period is the fraction
\begin{equation*}
\text{batting average} =
\frac{\#\text{hits}}{\#\text{at-bats}}
\end{equation*}
where “#hits” is the number of hits achieved and “#at-bats” is the number of attempts during that time period. For example, if a player gets 3 hits in 10 at-bats, then the player’s batting average is \(3/10 = 0.300 = 30\%\text{.}\)
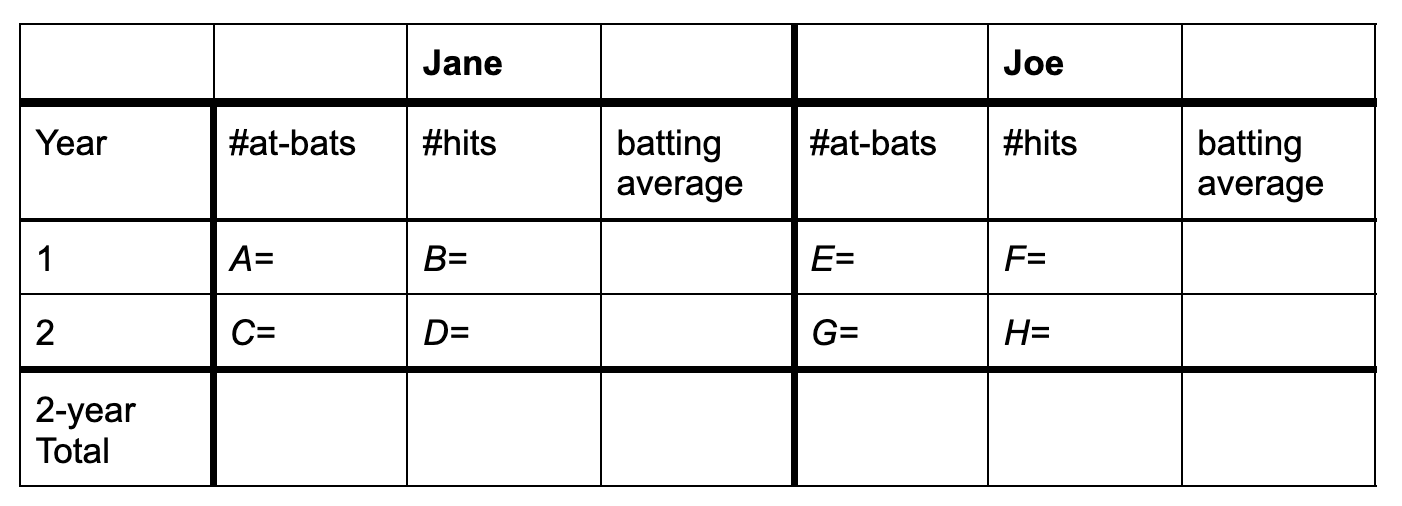
Question: Is it possible for a player to have the highest 1-year batting average for two years in a row, and yet there is some other batter who has a higher 2-year average?
Puzzle: If possible, find \(8\) numbers \(A,B,C,D,E,F,G,H\) to fill in the table below so that Jane’s batting average is higher than Joe’s in both years 1 and 2, but Joe’s 2-year batting average is higher than Jane’s. That is, you need to make \(\frac{B}{A} \gt \frac{F}{E}\text{,}\) make \(\frac{D}{C} \gt \frac{H}{G}\text{,}\) and make \(\frac{F+H}{E+G} \gt
\frac{B+D}{A+C}\text{.}\)