Section 0.2 Stereographic projection
Subsection 0.2.1 Stereographic projection \(S^1\to \R^+\)
Let \(S^1\) denote the unit circle in the \(x,y\)-plane.
Let \(N=(0,1)\) denote the "north pole" (that is, the point at the "top" of the unit circle). Given a point \(P=(x,y)\neq N\) on the unit circle, let \(s(P)\) denote the intersection of the line \(\overline{NP}\) with the \(x\)-axis. See Figure 0.2.1. The map \(s\colon S^1\setminus \{N\}\to \R\) given by this rule is called stereographic projection. Using similar triangles, it is easy to see that \(s(x,y)=\frac{x}{1-y}\text{.}\)
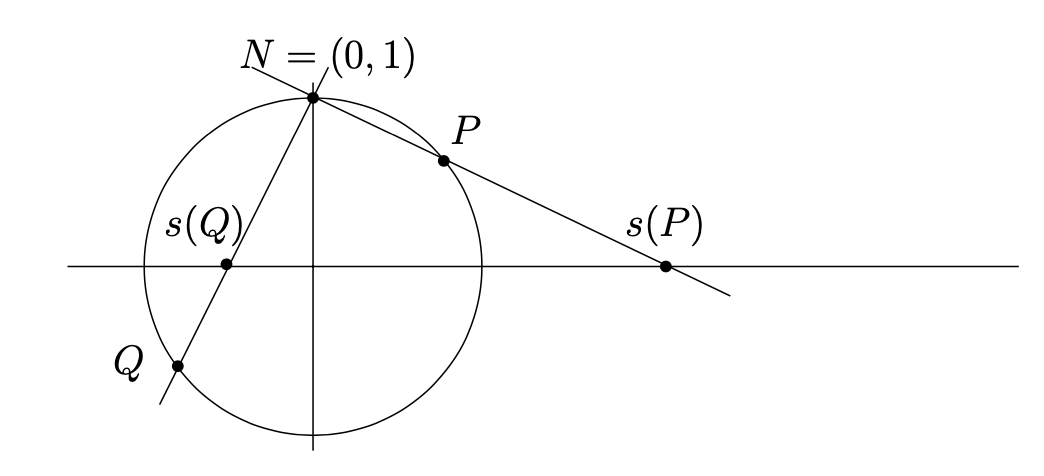
Checkpoint 0.2.2.
Draw the relevant similar triangles and verify the formula \(s(x,y) = \frac{x}{1-y}\text{.}\)
We extend stereographic projection to the entire unit circle as follows. We call the set
the extended real numbers, where "\(\infty\)" is an element that is not a real number. Now we define stereographic projection \(s\colon S^1 \to \R^+\) by
Subsection 0.2.2 Stereographic projection \(S^2\to \C^+\)
The definitions in the previous subsection extend naturally to higher dimensions. Here are the details for the main case of interest.
Let \(S^2\) denote the unit sphere in \(\R^3\text{.}\)
Let \(N=(0,0,1)\) denote the "north pole" (that is, the point at the "top" of the sphere, where the postive \(z\)-axis is "up"). Given a point \(P=(a,b,c)\neq N\) on the unit sphere, let \(s(P)\) denote the intersection of the line \(\overline{NP}\) with the \(x,y\)-plane, which we identify with the complex plane \(\C\text{.}\) See See Figure 0.2.3. The map \(s\colon S^2\setminus \{N\}\to \C\) given by this rule is called stereographic projection. Using similar triangles, it is easy to see that \(s(a,b,c)=\frac{a+ib}{1-c}\text{.}\)
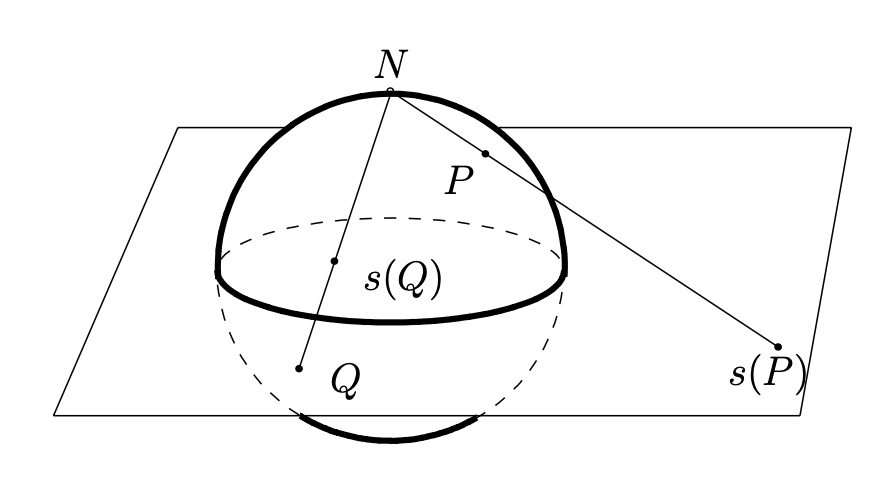
We extend stereographic projection to the entire unit sphere as follows. We call the set
the extended complex numbers, where "\(\infty\)" is an element that is not a complex number. Now we define stereographic projection \(s\colon S^2 \to \C^+\) by
Exercises 0.2.3 Exercises
Formulas for inverse stereographic projection.
It is intuitively clear that stereographic projection is a bijection. Make this rigorous by finding a formula for the inverse.
1.
For \(s\colon S^1\to \R^+\text{,}\) find a formula for \(s^{-1}\colon \R^+\to S^1\text{.}\) Find \(s^{-1}(3)\text{.}\)
2.
For \(s\colon S^2\to \C^+\text{,}\) find a formula for \(s^{-1}\colon \C^+\to S^2\text{.}\) Find \(s^{-1}(3+i)\text{.}\)
Liftings.
3.
Show that the map \(S^1\to S^1\) given by \((x,y)\to (x,-y)\) is a lifting of the map \(\R^+\to \R^+\) given by \(x\to 1/x\text{.}\)
4.
Show that the map \(S^2\to S^2\) given by \((a,b,c)\to (a,-b,-c)\) is a lifting of the map \(\C^+\to \C^+\) given by \(z\to 1/z\text{.}\)